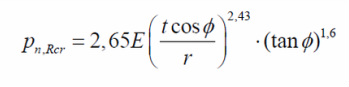Current Design Standards
|
EN 1993-4-1 E 2007, Design of Steel Structures (Silos) The current design standard for silos - guidance on the design of circular conical roofs EN 1993-4-1-7 proposes a formula for calculating the critical buckling external pressure:
From the very first glance this equation does not inspire confidence in one's possible design. It is clearly empirical (using exponents and coefficients with 2 decimal places), unsatisfactory and unreferenced. Although this formula is unreferenced (as is normal in design standards), its author is by lucky happenstance the supervisor of this research: Prof. Rotter, who clarified its genesis is an empirical fit from a sample of data that used a pinned boundary condition (reference to follow).
European Shell Buckling Recommendations: Chapter 13 (1th draft Mar 2011)
Conical shells and truncated conical shells under general loading Principal authors: R. Greiner and C. Poggi |
To produce these design recommendations, Greiner and Poggi conducted research very similar in nature to this thesis. However in choosing their range of variables and boundary conditions limited the results usefulness in designing shallow conical roofs, with a ring on the eaves. Indeed they acknowledge this, albeit in more general terms:
|
13.3.1 Conical shells under uniform external pressure on either the cone (uniform external pressure) or the cone and end closures (hydrostatic external pressure)
This section describes an alternative set of rules that may be used for the two special cases of uniform external pressure and hydrostatic external pressure. The background to these rules is described first,followed by appropriate expressions. An example then follows.The critical buckling resistance of cones or truncated cones under meridionally and circumferentially uniform external pressure was studied in a comprehensive numerical investigation by Koller (1980) and Resinger (1987). This study used linear buckling theory (LBA) using the in-house software developed by Esslinger et al. (1980) for the range of parameters 5° < B < 75° and 100 < r^(2)/t < 2000. The calculations covered both of the boundary condition combinations BC1-BC1 and BC2-BC2 and explored both the loading conditions of uniform external pressure and uniform hydrostatic external pressure.All the shells were supported at the larger end, causing the external pressure to induce meridional compression in the cone. As outlined in the commentary on 13.2.2.4(1), where the results for this support condition are used for the condition of support at the small end, the outcome is a conservative estimate of buckling strength. It may, however, be very conservative for cones with large apex half angles. |
|
Their options for design boundary conditions are either clamped (BC1) or pinned (BC2) - as described in EN 1993-4-1 5.2.2 These are unrealistic assumptions to make about particularly the radial restraint of silo roof supports. It is speculated that perhaps their application of interest was not silo roofs. Indeed this section of this chapter includes in the title "special cases", while much of the chapter focuses on rules appropriate to more steep cones and proposes an "equivalent cylinder" method. All these factors give the reader the impression that this research was intended to be applied somewhere other than silo roofs. Image (from EN 1993-4-1 8.4) assumes a pinned boundary condition applies to the top of the silo. |